[TOC]

list

set up ssh

add bash setting

First synchronize server time for v2ray

update tmux version by rpm file sudo rpm -i xxx.rpm

add tmux setting

setup v2fly and privoxy

setup docker

Table of contents

Background

1.Introduction

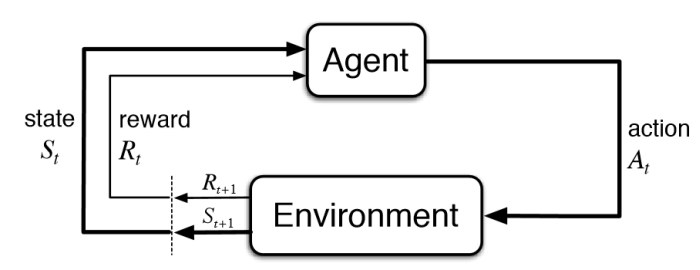
2.MDP

3. Planning by Dynamic Programming

4. model-free prediction

5 Model-free control

6 Value function approximation

7 Policy gradient methods

8.Integrating Learning and Planning

9. Exploration and Exploitation

10. Case Study: RL in Classic Games

Background

I started learning Reinforcement Learning 2018, and I first learn it from the book “Deep Reinforcement Learning Hands-On” by Maxim Lapan, that book tells me some high level concept of Reinforcement Learning and how to implement it by Pytorch step by step. But when I dig out more about Reinforcement Learning, I find the high level intuition is not enough, so I read the Reinforcement Learning An introduction by S.G, and following the courses Reinforcement Learning by David Silver, I got deeper understanding of RL. For the code implementation of the book and course, refer this Github repository.

Here is some of my notes when I taking the course, for some concepts and ideas that are hard to understand, I add some my own explanation and intuition on this post, and I omit some simple concepts on this note, hopefully this note will also help you to start your RL tour.

1.Introduction

RL feature

• reward signal
• feedback delay
• sequence not i.i.d
• action affect subsequent data

Why using discount reward?

• mathematically convenient
• avoids infinite returns in cyclic Markov processes
• we are not very confident about our prediction of reward, maybe we we only confident about some near future steps.
• human shows preference for immediate reward
• it is sometimes possible to use undiscounted reward

2.MDP

In MDP, reward is action reward, not state reward! \(R_s^a=E[R_{t+1}|S_t=s,A_t=a]\) Bellman Optimality Equation is non-linear , so we solve it by iteration methods.

3. Planning by Dynamic Programming

planning(clearly know the MDP(model) and try to find optimal policy)

prediction: given of MDP and policy, you output the value function(policy evaluation)

control: given MDP, output optimal value function and optimal policy(solving MDP)

• policy evaluation

• policy iteration

  • policy evaluation(k steps to converge)

  • policy improvement

    if we iterate policy once and once again and the MDP we already know, we will finally get the optimal policy(proved). so the policy iteration solve the MDP.

• value iteration

  1. value update (1 step policy evaluation)

  2. policy improvement(one step greedy based on updated value)

     iterate this also solve the MDP

asynchronous dynamic programming

• in-place dynamic programming(update the old value with new value immediately, not wait for all states new value)
• prioritized sweeping(based on value iteration error)
• real-time dynamic programming(run the game)

4. model-free prediction

model-free by sample

Monte-Carlo learning

every update of Monte-Carlo learning must have full episode

• First-Visit Monte-Carlo policy evaluation

  just run the agent following the policy the first time that state s is visited in an episode and do following calculation \(N(s)\gets N(s)+1 \\ S(s)\gets S(s)+G_t \\ V(s)=S(s)/N(s) \\ V(s)\to v_\pi \quad as \quad N(s) \to \infty\)

• Every-Visit Monte-Carlo policy evaluation

  just run the agent following the policy the every time(maybe there is a loop, a state can be visited more than one time) that state s is visited in an episode

  Incremental mean \(\begin{align} \mu_k &= \frac{1}{k}\sum_{j=1}^k x_j \\ &=\frac{1}{k}(x_k + \sum_{j=1}^{k-1} x_j) \\ &= \frac{1}{k}(x_k + (k-1)\mu_{k-1}) \\ &= \mu_{k-1}+\frac{1}{k}(x_k - \mu_{k-1}) \end{align}\)

  so by the incremental mean: \(N(S_t)\gets N(S_t)+1 \\ V(S_t)\gets V(S_t)+\frac{1}{N_t}(G_t-v(S_t)) \\\) In non-stationary problem, it can be useful to track a running mean, i.e. forget old episodes. \(V(S_t)\gets V(S_t)+\alpha(G_t-V(S_t))\)

Temporal-Difference Learning

learn form incomplete episodes, it gauss the reward. \(V(S_t)\gets V(S_t)+\alpha(G_t-V(S_t)) \\ V(s_t)\gets V(S_t)+\alpha(R_{t+1}+\gamma V(S_{t+1}) - V(S_t))\) TD target: $G_t=R_{t+1}+\gamma V(S_{t+1})$ TD(0)

TD error: $\delta_t = R_{t+1}+\gamma V(S_{t+1}) -V(S_t)$

TD($\lambda$)—balance between MC and TD

Let TD target look $n$ steps into the future, if $n$ is very large and the episode is terminal, then it’s Monte-Carlo \(\begin{align} G_t^{(n)}&=R_{t+1}+\gamma R_{t+2}+ ... + \gamma^{n-1} R_{t+n} + \gamma^nV(S_{t+n}) \\ V(S_t)&\gets V(S_t)+\alpha(G_t-V(S_t)) \end{align}\) Averaging n-step returns—forward TD($\lambda$) \(\begin{align} G_t^{\lambda} &= (1-\lambda)\sum_{n=1}^\infty \lambda^{n-1} G_t^{(n)} \\ V(S_t)&\gets V(S_t)+\alpha(G_t^\lambda-V(S_t)) \end{align}\) Eligibility traces, combine frequency heuristic and recency heuristic \(\begin{align} E_0(s) &= 0 \\ E_t(s) &= \gamma \lambda E_{t-1}(s) + 1(S_t=s) \end{align}\) TD($\lambda$)—TD(0) and $\lambda$ decayed Eligibility traces —backward TD($\lambda$) \(\begin{align} \delta_t &= R_{t+1}+\gamma V(S_{t+1}) -V(S_t) \\ V(s) &\gets V(s)+\alpha \delta_tE_t(s) \end{align}\) if the updates are offline (means in one episode, we always use the old value), then the sum of forward TD($\lambda$) is identical to the backward TD($\lambda$) \(\sum_{t=1}^T \alpha \delta_t E_t(s) = \sum_{t=1}^T \alpha(G_t^\lambda - V(S_t))1(S_t=s)\)

5 Model-free control

$\epsilon-greedy$ policy add exploration to make sure we are improving our policy and explore the ervironment.

On policy Monte-Carlo control

for every episode:

1. policy evaluation: Monte-Carlo policy evaluation $Q\approx q_\pi $
2. policy improvement: $\epsilon-greedy$ policy improvement based on $Q(s,a)$

Greedy in the limit with infinite exploration (GLIE) will find optimal solution.

GLIE Monte-Carlo control

for the $k$th episode, set $\epsilon \gets 1/k$ , finally $\epsilon_k$ reduce to zero, and it will get the optimal policy.

On-policy TD learning

Sarsa \(Q(S,A) \gets Q(S,A)+\alpha (R+ \gamma Q(S',A')-Q(S,A))\) On-Policy Sarsa:

for every time-step:

• policy evaluation: Sarsa, $Q\approx q_\pi $
• policy improvement: $\epsilon-greedy$ policy improvement based on $Q(s,a)$

forward n-step Sarsa —>Sarsa($\lambda$) just like TD($\lambda$)

Eligibility traces: \(\begin{align} E_0(s,a) &= 0 \\ E_t(s,a) &= \gamma \lambda E_{t-1}(s,a) + 1(S_t=s,A_t=a) \end{align}\) backward Sarsa($\lambda$) by adding eligibility traces

and every time step for all $(s,a)$ do following: \(\begin{align} \delta_t &= R_{t+1}+\gamma Q(S_{t+1},A_{t+1}) -Q(S_t,A_t) \\ Q(s,a) &\gets Q(s,a)+\alpha \delta_tE_t(s,a) \end{align}\)

The intuition of this that the current state action pair reward and value influence all other state action pairs, but it will influence the most frequent and recent pair more. and the $\lambda$ shows how much current influence others. if you only use one step Sarsa, every you get reward, it only update one state action pair, so it is slower. For more, refer Gridworld example on course-5.

Off-policy learning

Importance sampling

Importance sampling for off-policy TD \(V(s_t) \gets V(S_t) + \alpha \left(\frac{\pi(A_t|S_t)}{\mu(A_t|S_t)}(R_{t+1}+\gamma V(S_{t+1})-V(s_t)\right)\)

Q-learning

but consider alternative successor action(our target policy) $A’ \sim \pi(.|S_t)$ \(Q(S,A) \gets Q(S,A)+\alpha (R_{t+1} + \gamma Q(S_{t+1},A')-Q(S,A))\)

Here has something may hard to understand, so I explain it. no matter what action we actually do(behave) next, we just update Q according our target policy action, so finally we got the Q of target policy $\pi$.

Off-policy control with Q-Learning

• the target policy is greedy w.r.t Q(s,a) \(\pi(S_{t+1})=\underset{a'}{\arg\max} Q(S_{t+1},a)\)

• the behavior policy $\mu$ is e.g. $\epsilon -greedy$ w.r.t. Q(s,a) or maybe some totally random policy, it doesn’t matter for us since it is off-policy, and we only evaluate Q on $\pi$.

and Q-learning will converges to the optimal action-value function $Q(s,a) \to q_*(s,a)$

Q-learning can be used in off-policy learning, but it also can be used in on-policy learning!

For on-policy, if you using $\epsilon -greedy$ policy update, Sarsa is a good on-policy method, but you use Q-learning is fine since $\epsilon -greedy$ is similar to max Q policy, so you can make sure you explore most of policy action, so it is also efficient.

6 Value function approximation

Before this lecture, we talk about tabular learning since we have to maintain a Q table or value table etc.

Introduction

why

• state space is large
• continuous state space

Value function approximation

Approximator

• non-stationary (state values are changing since policy is changinng)
• non-i.i.d. (sample according policy)

Incremental method

Basic SGD for Value function approximation

• Stochastic Gradient descent
• feature vectors

• linear value function approximation \(\begin{align} \hat{v}(S,\pmb{w}) &= \pmb{x}(S)^T \pmb{w} = \sum_{j=1}^n \pmb{x}_j(S) \pmb{w}_j\\ J(\pmb {w}) &= E_\pi\left[(v_\pi(S)-\hat{v}(S,\pmb{w}))^2\right] \\ \Delta\pmb{w}&=-\frac{1}{2} \alpha \Delta_w J(\pmb{w}) \\ &=\alpha E_\pi \left[(v_\pi(S)-\hat{v}(S,\pmb{w})) \Delta_{\pmb{w}}\hat{v}(S,\pmb{w})\right] \\ \Delta\pmb{w}&=\alpha (v_\pi(S)-\hat{v}(S,\pmb{w})) \Delta_{\pmb{w}}\hat{v}(S,\pmb{w}) \\ & = \alpha (v_\pi(S)-\hat{v}(S,\pmb{w}))\pmb{x}(S) \end{align}\)

• Table lookup feature

table lookup is a special case of linear value function approximation, where w is the value of individual state.

Incremental prediction algorithms

How to supervise?

• For MC, the target is the return $G_t$ \(\Delta w = \alpha (G_t-\hat{v}(S_t,\pmb w))\Delta_w \hat{v}(S_t,w)\)

• For TD(0), the target is the TD target $R_{t+1} + \gamma \hat{v}(S_{t+1},\pmb{w})$ \(\Delta w = \alpha (R_{t+1} + \gamma \hat{v}(S_{t+1},\pmb{w})-\hat{v}(S_t,\pmb w))\Delta_w \hat{v}(S_t,w)\)

  here should notice that the TD target also has $\hat{v}(S_{t+1},\pmb{w})$, it contains w, but we do not calculate gradient of it, we just trust target at each time step, we only look forward, rather than look forward and backward at the same time. Otherwise it can not converge.

• For $TD(\lambda)$ , the target is $\lambda-return G_t^\lambda$ $$ \begin{align} \Delta\pmb{w} &= \alpha (G_t^\lambda-\hat{v}(S_t,\pmb w))\Delta_w \hat{v}(S_t,w) \

  \end{align} \(for backward view of Linear $TD(\lambda)$:\) \begin{align} \delta_t&= R_{t+1} + \gamma \hat{v}(S_{t+1},\pmb{w})-\hat{v}(S_t,\pmb{w})
  E_t &= \gamma \lambda E_{t-1} +\pmb{x}(S_t)
  \Delta \pmb{w}&=\alpha \delta_t E_t \end{align} $$

  here, unlike $E_t(s) = \gamma \lambda E_{t-1}(s) + 1(S_t=s)$ , we put $x(S_t)$ in $E_t$, so we don’t need remember all previous $x(S_t)$, note that in Linear TD, $\Delta \hat{v}(S_t,\pmb{w})$ is $x(S_t)$.

  here the eligibility traces is the state features, so the most recent state(state feature) have more weight, unlike TD(0), this is update all previous states simultaneously and the weight of state decayed by $\lambda$.

Control with value function approximation

policy evaluation: approximate policy evaluation, $\hat{q}(.,.,\pmb{w}) \approx q_\pi$

policy improvement: $\epsilon - greedy$ policy improvement.

Action-value function approximation \(\begin{align} \hat{q}(S,A,\pmb{w}) &\approx q_\pi(S,A)\\ J(\pmb {w}) &= E_\pi\left[(q_\pi(S,A)-\hat{q}(S,A,\pmb{w}))^2\right] \\ \Delta\pmb{w}&=-\frac{1}{2} \alpha \Delta_w J(\pmb{w}) \\ &=\alpha (q_\pi(S,A)-\hat{q}(S,A,\pmb{w}))\Delta_{\pmb{w}}\hat{q}(S,A,\pmb{w}) \end{align}\) Linear Action-value function approximation \(\begin{align}x(S,A) &= \begin{pmatrix} x_1(S,A)\\ \vdots \\ x_n(S,A) \end{pmatrix} \\ \hat{q}(S,A,\pmb{w}) &= \pmb{x}(S,A)^T \pmb{w} = \sum_{j=1}^n \pmb{x}_j(S,A) \pmb{w}_j\\ \Delta\pmb{w}&=\alpha (q_\pi(S,A)-\hat{q}(S,A,\pmb{w}))x(S,A) \end{align}\) The target is similar as value update, I’m lazy and do not write it down, you can refer it on book.

TD is not guarantee converge

convergence of gradient TD learning

Convergence of Control Algorithms

Batch reinforcement learning

motivation: try to fit the experiences

• given value function approximation $\hat{v}(s,\pmb{w} \approx v_\pi(s))$
• experience$\mathcal{D} $ consisting of$\langle state,value \rangle$ pairs:

• Least squares minimizing sum-squares error \(\begin{align} LS(\pmb{w})&=\sum_{t=1}^T(v_t^\pi -\hat{v}(s_t,\pmb{w}))^2 \\ &=\mathbb{E}_\mathcal{D}\left[(v^\pi-\hat{v}(s,\pmb{w}))^2\right] \end{align}\)

SGD with experience replay(de-correlate states)

1. sample state, vale form experience \(\langle s,v^\pi\rangle \sim \mathcal{D}\)

2. apply SGD update

Then converge to least squares solution

DQN (experience replay + Fixed Q-targets)(off-policy)

1. Take action $a_t$ according to $\epsilon - greedy$ policy to get experience $(s_t,a_t,r_{t+1},s_{t+1})$ store in $\mathcal{D}$

2. Sample random mini-batch of transitions $(s,s,r,s’)$

3. compute Q-learning targets w.r.t. old, fixed parameters $w^-$

4. optimize MSE between Q-network and Q-learning targets. \(\mathcal{L}_i(\mathrm{w}_i) = \mathbb{E}_{s,a,r,s' \sim \mathcal{D}_i}\left[\left(r+\gamma \max_{a'} Q(s',a';\mathrm{w^-})-Q(s,a,;\mathrm{w}_i)\right)^2\right]\)

5. using SGD update

On-linear Q-learning hard to converge, so why DQN converge?

• experience replay de-correlate state make it more like i.i.d.
• Fixed Q-targets make it stable

Least square evaluation

if the approximation function is linear and the feature space is small, we can solve the policy evaluation by least square directly.

• policy evaluation: evaluation by least squares Q-learning
• policy improvement: greedy policy improvement.

7 Policy gradient methods

Introduction

policy-based reinforcement learning

directly parametrize the policy \(\pi_\theta(s,a) = \mathcal(P)[a|s,\theta]\) advantages:

• better convergence properties
• effective in high-dimensional or continuous action spaces
• can learn stochastic policies

disadvantages:

• converge to a local rather then global optimum
• evaluating a policy is typically inefficient and high variance

policy gradient

Let $J(\theta)$ be policy objective function

find local maximum of policy objective function(value of policy) \(\Delta \theta = \alpha \Delta_\theta J(\theta)\) where $\Delta_\theta J(\theta)$ is the policy gradient \(\Delta_\theta J(\theta) = \begin{pmatrix} \frac{\partial J(\theta)}{\partial\theta_1 } \\ \vdots \\ \frac{\partial J(\theta)}{\partial\theta_n } \end{pmatrix}\) Score function trick \(\begin{align} \Delta_\theta\pi(s,a) &= \pi_\theta \frac{\Delta_\theta(s,a)}{\pi_\theta(s,a)} \\ &=\pi_\theta(s,a)\Delta_\theta \log\pi_\theta(s,a) \end{align}\) The score function is $\Delta_\theta \log\pi_\theta(s,a)$

policy

• Softmax policy for discrete actions
• Gaussian policy for continuous action spaces

for one-step MDPs apply score function trick \(\begin{align} J(\theta) & = \mathbb{E}_{\pi_\theta}[r] \\ & = \sum_{s\in \mathcal{S}} d(s) \sum _{a\in \mathcal{A}} \pi_\theta(s,a)\mathcal{R}_{s,a}\\ \Delta J(\theta) & = \sum_{s\in \mathcal{S}} d(s) \sum _{a\in \mathcal{A}} \pi_\theta(s,a)\Delta_\theta\log\pi_\theta(s,a)\mathcal{R}_{s,a} \\ & = \mathbb{E}_{\pi_\theta}[\Delta_\theta\log\pi_\theta(s,a)r] \end{align}\)

Policy gradient theorem

the policy gradient is \(\Delta_\theta J(\theta)= \mathbb{E}_{\pi_\theta}[\Delta_\theta\log\pi_\theta(s,a)Q^{\pi_\theta}(s,a)]\)

Monte-Carlo policy gradient(REINFORCE)

using return $v_t$ as an unbiased sample of $Q^{\pi_\theta}(s_t,a_t)$ \(\Delta\theta_t = \alpha\Delta_\theta\log\pi_\theta(s,a)v_t\\ v_t = G_t = r_{t+1}+\gamma r_{t+2}+\gamma^3 r_{t+3}...\) pseudo code

function REINFORCE Initialize $\theta$ arbitrarily

​ for each episode $ { s_1,a_1,r_2,…,s_{T-1},a_{T-1},R_T } \sim \pi_\theta$ do

​ for $t=1$ to $T-1$ do

​ $\theta \gets \theta+\alpha\Delta_\theta\log\pi_\theta(s,a)v_t$

​ end for

​ end for

​ return $\theta$

end function

REINFORCE has the high variance problem, since it get $v_t$ by sampling.

Actor-Critic policy gradient

Idea

use a critic to estimate the action-value function \(Q_w(s,a) \approx Q^{\pi_\theta}(s,a)\) Actor-Critic algorithm follow an approximate policy gradient \(\Delta_\theta J(\theta) \approx \mathbb{E}_{\pi_\theta}[\Delta_\theta\log\pi_\theta(s,a)Q_w(s,a)] \\ \Delta \theta= \alpha \Delta_\theta\log\pi_\theta(s,a)Q_w(s,a)\)

Action value actor-Critic

Using linear value fn approx. $Q_w(s,a) = \phi(s,a)^Tw$

• Critic Updates w by TD(0)
• Actor Updates $\theta$ by policy gradient

function QAC Initialize $s, \theta$

​ Sample $a \sim \pi_\theta$

​ for each step do

​ Sample reward $r=\mathcal{R}_s^a$; sample transition $s’ \sim \mathcal{P}_s^a$,.

​ Sample action $a’ \sim \pi_\theta(s’,a’)$

​ $\delta = r + \gamma Q_w(s’,a’)- Q_w(s,a)$

​ $\theta = \theta + \alpha \Delta_\theta \log \pi_\theta(s,a) Q_w(s,a)$

​ $w \gets w+\beta \delta\phi(s,a)$

​ $a \gets a’, s\gets s’$

​ end for

end function

So it seems that Value-based learning is a spacial case of actor-critic, since the greedy function based on Q is one spacial case of policy gradient, when we set the policy gradient step size very large, then the probability of the action which max Q will close to 1, and the others will close to 0, that is what greedy means.

Reducing variance using a baseline

• Subtract a baseline function $B(s)$ from the policy gradient

• This can reduce variance, without changing expectation \(\begin{align} \mathbb{E}_{\pi_\theta} [\Delta_\theta \log \pi_\theta(s,a)B(s)] &= \sum_{s \in \mathcal{S}}d^{\pi_\theta}(s)\sum_a \Delta_\theta \pi_\theta(s,a)B(s)\\ &= \sum_{s \in \mathcal{S}}d^{\pi_\theta}(s)B(s)\Delta_\theta \sum_{a\in \mathcal{A}} \pi_\theta(s,a)\\ & = \sum_{s \in \mathcal{S}}d^{\pi_\theta}(s)B(s)\Delta_\theta (1) \\ &=0 \end{align}\)

• a good baseline is the state value function $B(s) = V^{\pi_\theta}(s)$

• So we can rewrite the policy gradient using the advantage function $A^{\pi_\theta}(s,a)$ \(A^{\pi_\theta}(s,a) = Q^{\pi_\theta}(s,a) - V^{\pi_\theta}(s) \\ \Delta_\theta J(\theta) = \mathbb{E}_{\pi_\theta}[\Delta_\theta \log \pi_\theta(s,a)A^{\pi_\theta}(s,a)]\)

Actually, by using advantage function, we get rid of the variance between states, and it will make our policy network more stable.

So how to estimate the advantage function? you can using two network to estimate Q and V respectively, but it is more complicated. More commonly used is by bootstrapping.

• TD error

• TD error is an unbiased estimate(sample) of the advantage function \(\begin{align} \mathbb{E}_{\pi_\theta} & = \mathbb{E}_{\pi_\theta}[r + \gamma V^{\pi_\theta}(s')|s,a] - V^{\pi_\theta}(s) \\ & = Q^{\pi_\theta}(s,a)-V^{\pi_\theta}(s) \\ & = A^{\pi_\theta}(s,a) \end{align}\)

• So \(\Delta_\theta J(\theta) = \mathbb{E}_{\pi_\theta}[\Delta_\theta \log \pi_\theta(s,a)\delta^{\pi_\theta}]\)

• In practice, we can use an approximate TD error for one step \(\delta_v = r + \gamma V_v(s')-V_v(s)\)

• this approach only requires one set of critic parameters for v.

For Critic, we can plug in previous used methods in value approximation, such as MC, TD(0),TD($\lambda$) and TD($\lambda$) with eligibility traces.

• MC policy gradient, $\mathrm{v}_t$ is the true MC return. \(\Delta \theta = \alpha(\mathrm{v}_t - V_v(s_t))\Delta_\theta \log \pi_\theta(s_t,a_t)\)

• TD(0) \(\Delta \theta = \alpha(r + \gamma V_v(s_{t+1})-V_v(s_t))\Delta_\theta \log \pi_\theta(s_t,a_t)\)

• TD($\lambda$) \(\Delta \theta = \alpha(\mathrm{v}_t^\lambda + \gamma V_v(s_{t+1})-V_v(s_t))\Delta_\theta \log \pi_\theta(s_t,a_t)\)

• TD($\lambda$) with eligibility traces (backward-view) \(\begin{align} \delta & = r_{t+1} + \gamma V_V(s_{t+1}) -V_v(s_t) \\ e_{t+1} &= \lambda e_t + \Delta_\theta\log \pi_\theta(s,a) \\ \Delta \theta&= \alpha \theta e_t \end{align}\)

For continuous action space, we use Gauss to represent our policy, but Gauss is noisy, so it’s better to use deterministic policy(by just picking the mean) to reduce noise and make it easy to converge. This turns out the deterministic policy gradient(DPG) algorithm.

Deterministic policy gradient(off-policy)

Deterministic policy: \(a_t = \mu(s_t|\theta^\mu)\) Q network parametrize by $\theta^Q$ ,the distribution of states under behavior policy is $\rho^\beta$ \(\begin{align} L(\theta^Q) &= \mathbb{E}_{s_t \sim \rho^\beta, a_t \sim \beta,r_t\sim E}[(Q(s_t,a_t|\theta^Q)-y_t)^2] \\ y_t & = r(s_t,a_t)+\gamma Q(s_{t+1},\mu(s_{t+1})|\theta^Q) \end{align}\) policy network parametrize by $\theta^\mu$ \(\begin{align} J(\theta^\mu) & = \mathbb{E}_{s \sim \rho^\beta}[Q(s,a| \theta^Q)|_{s=s_t,a=\mu(s_t|\theta^\mu)}] \\ \Delta_{\theta^\mu}J &\approx \mathbb{E}_{s \sim \rho^\beta}[\Delta_{\theta_\mu} Q(s,a| \theta^Q)|_{s=s_t,a=\mu(s_t|\theta^\mu)}] \\ & = \mathbb{E}_{s \sim \rho^\beta}[\Delta Q(s,a| \theta^Q|_{s=s_t,a=\mu(s_t)}\Delta_{\theta_\mu}\mu(s|\theta^\mu)|s=s_t] \end{align}\) to make training more stable, we use target network for both critic network and actor network, and update them by soft update: \(soft\; update\left\{ \begin{aligned} \theta^{Q'} & \gets \tau\theta^Q+(1-\tau)\theta^{Q'} \\ \theta^{\mu'} & \gets \tau\theta^\mu+(1-\tau)\theta^{\mu'} \\ \end{aligned} \right.\) and we set $\tau$ very small to update parameters smoothly, e.g. $\tau = 0.001$.

In addition, we add some noise to deterministic action when we are exploring the environment to get experience. \(\mu'(s_t) = \mu(s_t|\theta_t^\mu)+\mathcal{N}_t\) where $\mathcal{N}$ is the noise, it can be chosen to suit the environment, e.g. Ornstein-Uhlenbeck noise.

8.Integrating Learning and Planning

Introduction

model-free RL

• no model
• Learn value function(and or policy) from experience

model-based RL

• learn a model from experience
• plan value function(and or policy) from model

Model $\mathcal{M} = \langle \mathcal{P}\eta, \mathcal{R}\eta \rangle$ \(S_{t+1} \sim \mathcal{P}_\eta(s_{t+1}|s_t,A_t) \\ R_{t+1} = \mathcal{R}_\eta(R_{t+1}|s_t,A_t)\) Model learning from experience ${S_1,A_1,R_2,…,S_T}$ bu supervised learning \(S_1, A_1 \to R_2, S_2 \\ S_2, A_2 \to R_3, S_3 \\ \vdots \\ S_{T-1}, A_{T-1} \to R_T, S_T\)

• $s,a \to r$ is a regression problem
• $s,s \to s’$ is a density estimation problem

Planning with a model

Sample-based planning

1. sample experience from model
2. apply model-free RL to samples
   • Monte-Carlo control
   • Sarsa
   • Q-learning

Performance of model-based RL is limited to optimal policy for approximate MDP

Integrated architectures

Integrating learning and planning—–Dyna

• Learning a model from real experience
• Learn and plan value function (and/or policy) from real and simulated experience

Simulation-Based Search

• Forward search select the best action by lookahead
• build a search tree withe the current state $s_t$ at the root
• solve the sub-MDP starting from now

Simulation-Based Search

1. Simulate episodes of experience for now with the model
2. Apply model-free RL to simulated episodes
   • Monte-Carlo control $\to$ Monte-Carlo search
   • Sarsa $\to$ TD search

Sample Monte-Carlo search

• Given a model $\mathcal{M}_v$ and a simulation policy $\pi$

• For each action $a \in \mathcal{A}$

  • Simulate K episodes from current(real) state $s_t$ \(\{s_t,a,R_{t+1}^k,S_{t+1}^k,A_{t+1}^k,...,s_T^k\}_{k=1}^K \sim \mathcal{M}_v,\pi\)

  • Evaluate action by mean return(Monte-Carlo evaluation)

  \[Q(s_t,a) = \frac{1}{K}\sum_{k=1}^K G_t \overset{\text{P}}{\to} q_\pi(s_t,a)\]

• Select current(real) action with maximum value \(a_t = \underset{a \in \mathcal{A}}{\arg\max} Q(S_{t},a)\)

Monte-Carlo tree search

• Given a model $\mathcal{M}_v$

• Simulate K episodes from current(real) state $s_t$ using current simulation policy $\pi$ \(\{s_t,A_t^k,R_{t+1}^k,S_{t+1}^k,A_{t+1}^k,...,s_T^k\}_{k=1}^K \sim \mathcal{M}_v,\pi\)

• Build a search tree containing visited states and actions

• Evaluate states Q(s,a) by mean return of episodes from s,a \(Q(s_t,a) = \frac{1}{N(s,a)}\sum_{k=1}^K \sum_{u=t}^T \mathbf{1}(s_u,A_u = s,a) G_u \overset{\text{P}}{\to} q_\pi(s_t,a)\)

• After search is finished, select current(real) action with maximum value in search tree \(a_t = \underset{a \in \mathcal{A}}{\arg\max} Q(S_{t},a)\)

• Each simulation consist of two phases(in-tree, out-of-tree)

  • Tree policy(improves): pick actions to maximise Q(s,a)
  • Default policy(fixed): pick action randomly

Here we update Q on the whole sub-tree, not only the current state. And after every episode of searching, we improve the policy based on the new update value, then start a new searching. With the searching progress, we exploit on the direction which is more promise to success since we keep updating our searching policy to that direction. In addition, we also need to explore a little bit the other direction, so we can apply MCTS with which action has the max Upper Confidence Bound(UCT) , that is idea of AlphaZero.

Temporal-Difference Search

e.g. update by Sarsa \(\Delta Q(S,A) = \alpha (R+\gamma Q(S',A') -Q(S,A))\) and you can also use a function approximation for simulated Q.

Dyna-2

• long-term memory(real experience)—TD learning
• Short-term(working) memory(simulated experience)—TD search & TD learning

9. Exploration and Exploitation

way to exploration

• random exploration
  • use Gaussian noise in continuous action space
  • $\epsilon - greedy$, random on $\epsilon$ probability
  • Softmax, select on action policy distribution
• optimism in the face of uncertainty———prefer to explore state/actions with highest uncertainty
  • Optimistic Initialization
  • UCB
  • Thompson sampling
• Information state space
  • Gittins indices
  • Bayes-adaptive MDPS

State-action exploration vs. parameter exploration

Multi-arm bandit

Total regret \(\begin{align} L_t &= \mathbb{E}\left[\sum_{\tau=1}^t V^*-Q(a_\tau)\right] \\ & \sum_{a \in \mathcal{A}}\mathbb{E}[N_t(a)](V^*-Q(a)) \\ &=\sum_{a \in \mathcal{A}}\mathbb{E}[N_t(a)]\Delta a \end{align}\) Optimistic Initialization

• initialize Q(a) to high value
• Then act greedily
• turns out linear regret

$\epsilon - greedy$

• turns out linear regret

decay $\epsilon - greedy$

• sub-linear regret(need know gaps), if you tune it very well and find it just on the gap, it is good, otherwise, it maybe bad.

the regret has a low bound, it is a log bound

The performance of any algorithm is determined by similarity between optimal arm and other arms \(\lim_{t \to \infty}L_t \ge \log t\sum_{a|\Delta a>0} \frac{\Delta a}{KL(\mathcal{R}^a||\mathcal{R}^{a_*})}\)

Optimism in the Face of Uncertainty

Upper Confidence Bounds(UCB)

• Estimate an upper confidence $U_t(a)$ for each action value

• Such that $q(a) \leq Q_t(a)+U_t(a)$ with high probability

• The upper confidence depend on the number of times N(s) has been sampled

• Select action maximizing Upper Confidence Bounds(UCB) \(A_t =\underset{a \in \mathcal{A}}{\arg\max} [Q(S_{t},a)+U_t(a)]\)

Theorem(Hoeffding’s Inequality)

let $x_1,…,X_t$ be i.i.d. random variables in[0,1], and let $\overline{X} = \frac{1}{\tau}\sum_{\tau=1}^tX_\tau$ be the sample mean. Then \(\mathbb{P}[\mathbb{E}[X]> \overline{X}_t+u] \leq e^{-2tu^2}\)

we apply the Hoeffding’s Inequality to rewards of the bandit conditioned on selecting action a \(\mathbb{P}[ Q(a)> Q(a)+U_t(a)] \leq e^{-2N_t(a)U_t(a)^2}\)

• Pack a probability p that true value exceeds UCB

• Then solve for $U_t(a)$ \(\begin{align} e^{-2N_t(a)U_t(a)^2} = p \\ \\ U_t(a)=\sqrt{\frac{-\log p}{2N_t(a)}} \end{align}\)

• Reduce p as we observe more rewards, e.g. $p = t^{-4}$ \(U_t(a)=\sqrt{\frac{2\log t}{N_t(a)}}\)

• Make sure we select optimal action as $t \to \infty$

This leads to the UCB1 algorithm \(A_t =\underset{a \in \mathcal{A}}{\arg\max} \left[Q(S_{t},a)+\sqrt{\frac{2\log t}{N_t(a)}}\right]\) The UCB algorithm achieves logarithmic asymptotic total regret \(\lim_{t\to\infty}L_t \leq 8\log t\sum_{a|\Delta>0}\Delta a\) Bayesian Bandits

Probability matching—Thompson sampling—optimal for one sample, but may not good for MDP.

Solving Information State Space Bandits—MDP

define MDP on information state space

MDP

UCB \(A_t =\underset{a \in \mathcal{A}}{\arg\max} [Q(S_{t},a)+U_t(S_t,a)]\) R-Max algorithm

10. Case Study: RL in Classic Games

TBA.

zip and unzip on Linux

Zip file

unzip filename.zip

tar command

for detail refer tar –help

for tar version later than 1.15, it can automatically recognize the file format, there is no need to clear format in command, just use

tar -xvf filename.tar.xxx

filename.tar.gz

tar -zxvf filename.tar.gz

zip file

tar -cf archive.tar foo 

Set up color through ssh

you only need to add these lines to .bashrc

# set a fancy prompt (non-color, unless we know we "want" color)
case "$TERM" in
    xterm-color) color_prompt=yes;;
esac

# uncomment for a colored prompt, if the terminal has the capability; turned
# off by default to not distract the user: the focus in a terminal window
# should be on the output of commands, not on the prompt
force_color_prompt=yes

if [ -n "$force_color_prompt" ]; then
    if [ -x /usr/bin/tput ] && tput setaf 1 >&/dev/null; then
	# We have color support; assume it's compliant with Ecma-48
	# (ISO/IEC-6429). (Lack of such support is extremely rare, and such
	# a case would tend to support setf rather than setaf.)
	color_prompt=yes
    else
	color_prompt=
    fi
fi

if [ "$color_prompt" = yes ]; then
    PS1='${debian_chroot:+($debian_chroot)}\[\033[01;32m\]\u@\h\[\033[00m\]:\[\033[01;34m\]\w\[\033[00m\]\$ '
else
    PS1='${debian_chroot:+($debian_chroot)}\u@\h:\w\$ '
fi
unset color_prompt force_color_prompt

# If this is an xterm set the title to user@host:dir
case "$TERM" in
xterm*|rxvt*)
    PS1="\[\e]0;${debian_chroot:+($debian_chroot)}\u@\h: \w\a\]$PS1"
    ;;
*)
    ;;
esac

# enable color support of ls and also add handy aliases
if [ -x /usr/bin/dircolors ]; then
    test -r ~/.dircolors && eval "$(dircolors -b ~/.dircolors)" || eval "$(dircolors -b)"
    alias ls='ls --color=auto'
    #alias dir='dir --color=auto'
    #alias vdir='vdir --color=auto'

    alias grep='grep --color=auto'
    alias fgrep='fgrep --color=auto'
    alias egrep='egrep --color=auto'
fi

# for more fancy prompt
# PS1='\[\033[1;36m\]\u\[\033[1;31m\]@\[\033[1;32m\]\h:\[\033[1;35m\]\w\[\033[1;31m\]\$\[\033[0m\] '

Understanding Alpha Go, Alpha Zero and Monte Carlo Tree Search

Basic

• Search: Games, Minimax, and Alpha-Beta - lecture by Patrick H. Winston
• Monte Carlo Tree Search

Monte Carlo Tree Search

Upper Confidence Bound applied to trees(UCT)

​ where $v_i$ is the child node of $v$, $c$ is the trade-off factor of exploration and exploitation. $Q(v)$ is the total simulation reward and $N(v)$ is the total number of visits.

​ The searching procedure is expanded by UCT policy. In UCT, the first item is called win ratio, which is exploitation component, and the second one is exploration component.

Alpha Go & Alpha Zero

References

Monte Carlo Tree Search – beginners guide

RNN

The idea of an RNN is a network with fixed input and output, which is being applied to the sequence of objects and can pass information along this sequence. This information is called hidden state and is normally just a vector of numbers of some size.

Unfold RNN (unfold by time)

RNN produce different output for the same input in different contexts, RNNs can be seen as a standard building block of the systems that need to process variable-length input.

long short-term memory networks (LSTM)

LSTM first proposed in 1997. It performs good in speech recognition and text-to-speech synthesis.

gated recurrent units(GRU)

GRU proposed in 2014, Their performance on polyphonic music modeling and speech signal modeling was found to be similar to that of long short-term memory. They have fewer parameters than LSTM, as they lack an output gate.

encoder-decoder

use an RNN to process an input sequence and encode this sequence into some fixed-length representation. This RNN is called an encoder. Then you feed the encoded vector into another RNN, called a decoder, which has to produce the resulting sequence. It is widely used in machine translation.

curriculum learning mode

attention mechanism

seq2seq (picture from Google)

CNN dimension

convolution operation: share the convolution core

output size is: \(O = (n-f+1) * (n-f+1)\) where input size is $n\times n$, convolution core size is $f\times f$.

terms: channels, strides, padding

• channels: look following picture, the input is $6\times 6\times 3$ RGB picture, and we use $3\times 3\times 3$ convolution core, the last 3 is the channel number of convolution core, which is same as the input picture channel number. During convolution, we multiply the input and add it together , so the output size is $4\times 4\times 1$.

and we often not only use only one convolution core, we use multi-cores to get multi-features form input. The following image shows the situation that we use two cores, so the output size is $4\times 4\times 2$. Then the input channel of following convolution layer is 2.

output size: \(O =(n-f+1) * (n-f+1) * C_o\) where $C_o$ is the number of convolution cores(output channel).

• padding: add data to the border of input, often to make sure the output size is same as input.

  

  output size: \(O =(n+2p-f+1) * (n+2p-f+1) * C_o\) where $p$ is padding length of one side. e.g. the last picture $p = 1$.

  if you want to make sure output size is same as input, set $p = (f-1)/2$, since at this moment, $n-f+2p+1 = n$.

• strides: stripe is the moving step length of convolution core.

output size: \(O =(\frac{n+2p-f}{s}+1) * (\frac{n+2p-f}{s}+1) * C_o\) where $s$ is stride length.

demo

So lets get the demo’s output size:

expose Intranet machine to outside

condition: you have a Intranet machine(mabe the machine is in your company), and it do not have a pubic IP, and you want to visit your machine at your home or anywhere can connect Internet.

requirements: you need have a server with a public IP.

Howto:

Here, we use a open source named frp, your can choose the version of your operate system and download it from Github repo.

and we just describe the bash ssh function, more functions you can refer frp Readme file

SSH Usage

Put frps and frps.ini to your server with public IP.

Put frpc and frpc.ini to your server in LAN.

Access your computer in LAN by SSH

1. Modify frps.ini:

# frps.ini
[common]
bind_port = 7000

1. Start frps on background:

nohup ./frps -c ./frps.ini > /dev/null 2>&1 &

1. Modify frpc.ini, server_addr is your frps’s server IP:

# frpc.ini
[common]
server_addr = x.x.x.x
server_port = 7000

[ssh]
type = tcp
local_ip = 127.0.0.1
local_port = 22
remote_port = 6000

1. Start frpc:

./frpc -c ./frpc.ini

1. Connect to server in LAN by ssh assuming that username is test:

ssh -oPort=6000 test@x.x.x.x

Notice:

• you must open your port used in frs( eg. 7000,6000) on your server, usually it is on the setting of firewall rules.
• Every client need one remote_port to map.

and if you want to visit Jupyter notebook and tensorboard, you only need to add a new port to frpc, and then visit https://x.x.x.x:port

ssh on your mobile phone

here we just describe the method on IOS. we use a software named Termius, the basic ssh function of it is free.

1. open the Termius
2. Hosts—>add new—->input you remote ip, ssh username, password and save it
3. just connect the host

if you’d like to use ssh on Termius,

1. open the Termius
2. Keychain—>add key(or use existed one)
3. edit it and copy the public key
4. append the Termius public key to your server’s ~/.ssh/authorized_keys file
5. on Termius, edit your host and add the key your created in Keychain ,and then save it
6. connect server and enjoy it!

Table of contents

• Basic
• Cross-entropy method
• Tabular Learning
• DQN
• Policy Gradients
• DRL in NLP
• NN functions

basic

Markov Decision Process (MDP)

environment, state, observation, reward, action, agent

Policy

State-value function

where $r_t$ is the reward at step $t$, $\gamma\in[0,1]$ is the discount-rate.

Value function

Action value function

method classification

• model-based: previous observation predict following rewards and observations
• model-free: train it by intuition
• police-based: directly approximating the policy of the agent
• value-based: the agent calculates the value of every possible action
• off police: the ability of the method to learn on old historical data (obtained
• on police: requires fresh data obtained from the environment

Police-based method

just like a classification problem

• NN input: observation
• NN output: distribution of actions
• agent: random choose action base on distribution of actions(police)

cross-entropy method

steps:

1. Play N number of episodes using our current model and environment.
2. Calculate the total reward for every episode and decide on a reward boundary. Usually, we use some percentile of all rewards, such as 50th or 70th.
3. Throw away all episodes with a reward below the boundary.
4. Train on the remaining “elite” episodes using observations as the input and issued actions as the desired output.
5. Repeat from step 1 until we become satisfied with the result.

use cross-entropy loss function as loss function

drawback: Cross-entropy methods have difficult to understand which step or which state is good and which is not good, it just know overall this episode is better or not

tabular learning

Why using Q but not V?

​ if I know the value of current state, I know the state is good or not, but I don’t know how to choose next action, even I know the V of all next state, I can not directly know which action i need to do, so we decide action base on Q.

​ if I know Q of all available action, we just choose the action which has max Q, then this action surely has max V according the definition of V(the relationship of Q and V).

The value iteration in the Env with a loop

If there is no $\gamma (\gamma = 1)$ and the environment has a loop, the value of state will be infinite.

problems in Q-learning

• state is not discrete
• state space is is very large

• don’t know probability of action and reward matrix (P(s’,r

  s,a)).

Value iteration

Reward table

• index: “source state” + “action” + “target state”
• value: reward

Transition table

• index: “state” + “action”
• value: index: state value: counts

Value table

• index: state
• value: value of state

Steps

1. random action to build reward and transitions table

2. perform a value iteration loop over all state

3. play several full episodes to choose the best action using the updated value table, at the same time, update reward and transitions table using new data.

**Problems of separating training and testing **: When using the previous steps, you actually separate training and testing, it may has another problem, since the task may be difficult,using random action is hard to reach the final state, so you may lack some states which are near the final step. So, maybe you should conduct training and testing at the same time, and add some exploit into testing.

Q-learning

Different to value iteration,Q-learn change the value table to Q value table:

Q value table

• index: “state” + “action”
• value: action value(Q)

Here : \(V(s) = \mathop{\arg\max}_{a}Q(a,s)\)

deep q-learning

DQN:

input: state

output: all action(n actions) value of input state

classification: off policy, value based and model free

problems:

• how to balance explore&exploit
• data is not independent and identically distributed(i.i.d), which is required for neural network training.
• may partially observable MDPs (POMDP)

Basic tricks in Deepmind 2015 paper:

• $\epsilon$-greedy to deal with explore&exploit
• replay buffer and target network to deal with i.i.d,
  • replay buffer make it more random, it random select experience in a replay buffer
  • target network isolated the influence of nearby Q during training
• several observations as a state to deal with POMDP

Double DQN

Idea: Choosing actions for the next state using the trained network but taking values of Q from the target net.

Noisy Networks

Idea: Add a noise to the weights of fully-connected layers of the network and adjust the parameters of this noise during training using back propagation. (to replace $\epsilon$-greedy and improve performance)

Prioritized replay buffer

Idea: This method tries to improve the efficiency of samples in the replay buffer by prioritizing those samples according to the training loss.

Trick: using loss weight to compensated the distribution bias introduced by priorities.

Dueling DQN

Idea: The Q-values Q(s, a) our network is trying to approximate can be divided into quantities: the value of the state V(s) and the advantage of actions in this state A(s, a).

Trick: the mean value of the advantage of any state to be zero.

Categorical DQN

Idea: Train the probability distribution of action Q-value rather than the action Q-value

Tricks:

• using generic parametric distribution that is basically a fixed amount of values placed regularly on a values range. every fixed amount of values range calls atom.

• use loss Kullback- Leibler (KL)-divergence

policy gradients

REINFORCE

idea

Policy Gradient \(\Delta J \approx E[Q(s,a)\Delta\log\pi(a|s)] \label{l5}\) loss formula \(loss = -Q(s,a)\log\pi(a|s) \label{l6}\) Increase the probability of actions that have given us good total reward and decrease the probability of actions with bad final outcomes. \({split} \pi(a|s)>0\\ -\log\pi(a|s) > 0 \label{l7}\) {split}

problems:

• one training need full episodes since require Q from finished episode

• High gradients variance, long steps episode have larger Q than short one

• converge to some locally-optimal policy since lack of exploration
• not i.i.d. Correlation between samples

basic tricks

• learning Q(Actor-Critic)
• subtracting a value called baseline from the Q to avoid high gradients variance
• in order to prevent our agent from being stuck in the local minimum, subtracting the entropy from the loss function, punishing the agent for being too certain about the action to take.
• parallel environments to reduce correlation, steps from different environments.

Actor- Critic

Using equation \ref{Q_update} to train V(s) (Critic) and equation \ref{pg_update} to train policy. We call A(s,a) as advantage, so it is advantage Actor- Critic (A2C).

Idea: The scale of our gradient will be just advantage A(s, a), we use another neural network, which will approximate V(s) for every observation.

Implementation

In practice, policy and value networks partially overlap, mostly due to the efficiency and convergence considerations. In this case, policy and value are implemented as different heads of the network, taking the output from the common body and transforming it into the probability distribution and a single number representing the value of the state. This helps both networks to share low-level features, but combine them in a different way.

Tricks

• add entropy bonus to loss function \(H_{entropy} = -\Sigma (\pi \log\pi) \\ Loss_{entropy} = \beta*\Sigma_i (\pi_\theta(s_i)*\log\pi_\theta(s_i)) \label{l10}\)

  the loss function of entropy has a minimum when probability distribution is uniform, so by adding it to the loss function, we’re pushing our agent away from being too certain about its actions.

• using several environments to improve stability

• gradient clipping to prevents our gradients at optimization stage from becoming too large and pushing our policy too far.

Total Loss function

Finally, our loss is the sum of PG, value and entropy loss \(Loss =Loss_{policy}+Loss_{value}+Loss_{entropy}\)

Asynchronous Advantage Actor-Critic(A3C)

Just using parallel envs to speed up training, there will be some code level tricks to speed up by fully utilizing multiple GPUs and CPUs. For more details, ref some open source implementations on Github.

Deep Reinforcement Learning (Deep RL) in Natural Language Processing (NLP)

Basic concepts in NLP

• Recurrent Neural Networks (RNNs)
• word embeddings
• the seq2seq model
• Recurrent models of visual attention (original paper NIPS 2014)

Ref. CS224d for more about NLP.

RNN

The idea of an RNN is a network with fixed input and output, which is being applied to the sequence of objects and can pass information along this sequence. This information is called hidden state and is normally just a vector of numbers of some size.

Unfold RNN (unfold by time)

RNN produce different output for the same input in different contexts, RNNs can be seen as a standard building block of the systems that need to process variable-length input.

LSTM

Word embedding(word2vec)

Word and phrase embeddings, is the collective name for a set of language modeling and feature learning techniques in natural language processing (NLP) where words or phrases from the vocabulary are mapped to vectors of real numbers. Conceptually it involves a mathematical embedding from a space with one dimension per word to a continuous vector space with a much lower dimension.

Methods to generate this mapping include neural networks, dimensionality reduction on the word co-occurrence matrix, probabilistic models, explainable knowledge base method, and explicit representation in terms of the context in which words appear.

Word embedding is good for NLP tasks such as syntactic parsing and sentiment analysis. Ref word embedding for details.

You can use some pretrained dataset or get it by training your own dataset.

Encoder-Decoder(seq2seq)

use an RNN to process an input sequence and encode this sequence into some fixed-length representation. This RNN is called an encoder. Then you feed the encoded vector into another RNN, called a decoder, which has to produce the resulting sequence. It is widely used in machine translation.

• teacher-forcing mode: decoder input is the target reference

• curriculum learning mode: decoder input is the last out put of previous decoder

  curriculum learning mode

• attention mechanism

seq2seq (picture from Google)
attention mechanism (this picture from zhihu)

RL in seq2seq

• sampling from probability distribution, instead of learning some average result
• score is not differentiable, we still can use PG to update, use score as scale
• introducing stochasticity into the process of decoding when dataset is limited
• use argmax score as baseline of Q

DDPG

TBC.

Model-based RL

TBC.

nn functions

sigmoid

It transfer a value input to (0,1)

softmax

In short, It transfer K-dimensional vector input to (0,1)

In mathematics, the softmax function, or normalized exponential function, is a generalization of the logistic function that “squashes” a K-dimensional vector z of arbitrary real values to a K-dimensional vector \sigma(z) of real values, where each entry is in the range (0, 1), and all the entries add up to 1.

tanh

It transfer a value input to (-1,1)

relu

Reference

• Maxim Lapan, Deep Reinforcement Learning Hands-On 2018

• Mnih V, Kavukcuoglu K, Silver D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540): 529.
• Mnih V, Heess N, Graves A. Recurrent models of visual attention[C]//Advances in neural information processing systems. 2014: 2204-2212.
• Paszke, Adam and Gross, etc. Automatic differentiation in PyTorch, 2017

python managers

python version manage

• pyenv and the commands can find here
• Anaconda

python package manager

• pip

• conda

  refer this article to get fully understand of python version management

python virtual environment

• virtualenv—tutorial

  virtualenv ENV
  source /path/to/ENV/bin/activate
  deactivate
  

• conda—tutorial

  conda create --name env_name package
  source activate env_name
  source deactivate
  

[TOC]

Server ip

1. first log the jump server:172.16.101.136

2. then visit 172.16.0.248 on jump server

Port forward：

ssh -N -f -L 2222:172.16.0.248:22 lidd@172.16.101.136
ssh lidd@localhost -p 2222

To connect network

1. sudo vim /etc/resolvconf/resolv.conf.d/base
2. add ‘nameserver 8.8.8.8’ to file
3. resolvconf -u

ssh key setting

​ You run the first command once to set up your public/private key pair and then you run the second command once for each host you want to connect to.

ssh-keygen
ssh-copy-id hostname

or you can do it manually by append your local xxx.pub key to your server’s ~/.ssh/authorized_keys file.

for details, refer SSH login without password

Transparent Multi-hop SSH

• your computer: dd
• your jump machine: jumper
• remote server: g-server

1. subl ~/.ssh/config

2. add following to it

   Host jumper ​ user lidd ​ HostName 172.16.101.136

   Host g-serversubl ​ user lidd ProxyCommand ssh -q jumper nc -q0 172.16.0.248 22

   Then you can direct use

   ssh g-server
   ssh -X g-server
   scp path/to/local/file g-server:path/to/remote/file
   

3. improve speed

   • mkdir ~/.ssh/tmpmkdir ~/.ssh/tmp

   • add these two lines at the start of your ~/.ssh/config (make sure to use your username in place of ‘YOUR-NAME’):

   ControlMaster auto ControlPath /home/YOUR-NAME/.ssh/tmp/%h_%p_%r

sshfs mount

mount

sshfs lidd@localhost:/home/lidd /home/dd/remote -p 2222		# when using port forward

sshfs g-server:/home/lidd /home/dd/remote					# when using nc

unmount

fusermount -u /home/dd/remote or umount /home/dd/remote

auto mount on start up

note: this is very dangerous!!! if the network has some problem, then you can not turn on your computer since system cannot find remote disk

add

sshfs#lidd@localhost:/home/lidd /home/dd/remote -p 2222 fuse defaults,auto,allow_other 0 0

to file ‘/etc/fstab’

Ref. For more info about jump host configuration, refer Jump Hosts

Ref. SSHMenu Articles

jupyter and tensorboard configuration

Visit jupyter notebook without token and open as public server

1. on server run jupyter notebook --generate-config

2. open ipython and run

   In [1]: from notebook.auth import passwd
   In [2]: passwd()
   Enter password: 
   Verify password: 
   Out[2]: 'sha1:ce23d945972f:34769685a7ccd3d08c84a18c63968a41f1140274'In [1]: from 
   

   Here, the password is for you to log in jupyer notebook to replace the random token on browser

3. vi ~/.jupyter/jupyter_notebook_config.py
   

   add following text to it

   # Set ip to '0.0.0.0' to bind on all interfaces (ips) for the public server
   c.NotebookApp.ip = '0.0.0.0'
   c.NotebookApp.password = u'sha1:0xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx' #the output of last step
   c.NotebookApp.open_browser = False
   c.NotebookApp.port =8889 #指定一个端口
   

4. visit jupyter by https://localhost:8889 or https://serverip:8889 and input the password you set before and enjoy it!

tensorboard open as public server

run on server

tensorboard --logdir=runs --host=0.0.0.0 --port=6006

Jupyter notebook and tensorboard on remote

In following examples,

jumper ip: 172.16.101.136

server ip: 172.16.0.248

you have a user named lidd in both machine.

if you configured it as a public server

Set ip to c.NotebookApp.ip = '0.0.0.0' to bind on all interfaces (ips) for the public server

• M1

on your computer add following to ‘./ssh/config’

Host jupyter ​ HostName 172.16.101.136 ​ LocalForward 8889 172.16.0.248:8889 ​ User lidd

Host tensorboard ​ HostName 172.16.101.136 ​ LocalForward 8008 172.16.0.248:6006 ​ User lidd

then run

ssh -f -N jupyter
ssh -f -N tensorboard

• M2

or just run

ssh -N -f -L 8889:172.16.0.248:8889 lidd@172.16.101.136

if you didn’t configure it as a public server, there is a jumper

note: in this case, jupyter notebook only can be access by [localhost], so we must forward ssh tunnel twice

Method 1：

1. on jumper :

   add following to ‘./ssh/config’

   Host jupyter_dd
   	HostName 172.16.0.248
   	LocalForward 10048 localhost:8889
   	User lidd
   Host tensorboard_dd 
   	HostName 172.16.0.248
   	LocalForward 10049 127.0.0.1:6006
   	User lidd
   

   and then run

   ssh -f -N jupyter_dd
   ssh -f -N tensorboard_dd
   

   Here, I am not sure why tensorboard need ‘127.0.0.1’ but not ‘localhost’

2. on your computer add following to ‘./ssh/config’

   Host jupyter
   	HostName 172.16.101.136
   	LocalForward 8889 localhost:10048
   	User lidd
   Host tensorboard
   	HostName 172.16.101.136
   	LocalForward 8008 localhost:10049
   	User lidd
   

   and then run

   ssh -f -N jupyter
   ssh -f -N tensorboard
   

Method ２：

1. on jumper :

   ssh -f -N -L 10048:localhost:8889 lidd@172.16.0.248
   

2. on your computer

   ssh -f -N -L 8889:localhost:10048 lidd@172.16.101.136
   

   then run jupyter notebook and tensorboard on server by running

   jupyter notebook --no-browser --port=8889 upyter notebook --no-browser --port=8889
   tensorboard --logdir=runs --host localhost 
   

   then you can visit jupyter by https://localhost:8889 and https://locahost:8008 , but you have to input token on jupyter

   notice: if you use relative dirctionary, you must run tensorboard in the dirctionary, otherwise tensorboard con’t find your log data to show

ref. SSHMenu Articles

In case you do not have a user account of jumper machine

Method 1

In case that the jumper machine already forwards server’s ssh (22) port to other opening port, let’s say port 12345. But you do not have a user in jumper machine. Then you can do follows:

ssh -f -N -L 9988:0.0.0.0:9600 -p 12345 server_username@jumper_ip

on your server machine, you create a service on port 9600, and it will be forwarded to http://localhost:9988.

here is the flow:

   service:9600
        |
        |
        |
        V     22           12345
server----------->jumper----------->local_machine:9988

Method 2

use a ssh socks proxy

ssh -f -N -D 9988 -p 12345 server_username@jumper_ip

Then you have to set you browser proxy to socks5 with 127.0.0.1:9988. By doing so, you can access you remote server ports by visiting http://localhost:romete_port. and you can also surf Internet by using the this proxy server. If you do not want connect Internet by this proxy, you can set up proxy rules only forlocalhost .

Stop tunnel

ps aux | grep ssh

and then find and kill the forwarding process

ref ssh ssh tunnel

Forward TCP/UDP

ssh usually run on TCP, if you have a jumper machine, you want the jumper forward internal ssh connection to the outside, you can just forward the TCP connection, This is done by iptables.

                22                           12345
machine A--------------jumper machine B----------------outside

Let’s say you internal machine A using ssh connection to the jumper machine B with port 22, you want to ssh the port 12345 on machine B to ssh machine A directly.

iptables -t nat -A PREROUTING -p tcp -i <WAN interface> --dport 12345 -j DNAT --to-destination <machine-A-IP>:22
iptables -A FORWARD -p tcp -d <machine-A-IP> --dport 22 -m state --state NEW,ESTABLISHED,RELATED -j ACCEPT

WAN interface is the WAN net card name, e.g. eth0. The first rule rewrites the destination address, the second allows the modified packet to be delivered to its destination. This assumes that machine A’s default gateway is machine B.

you can check by ip route command.

set up cuda on server

download

cuda_9.0.176_384.81_linux.run

NVIDIA-Linux-x86_64-384.145.run

libcudnn7_7.3.1.20-1+cuda9.0_amd64.deb

libcudnn7-dev_7.3.1.20-1+cuda9.0_amd64.deb

uninstall old version ref nvidia

sudo /usr/local/cuda-X.Y/bin/uninstall_cuda_X.Y.pl
sudo /usr/bin/nvidia-uninstall

install Nvidia driver and cuda with --no-opengl-files to make sure xvfb-run can used on server

sudo chmod +x cuda_9.0.176_384.81_linux.run  
sudo chmod +x NVIDIA-Linux-x86_64-384.145.run
sudo ./NVIDIA-Linux-x86_64-384.145.run --no-opengl-files
sudo ./cuda_9.0.176_384.81_linux.run   --no-opengl-files
echo "export PATH=$PATH:/usr/local/cuda-9.0/bin" >> ~/.bashrc
echo "export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:/usr/local/cuda-9.0/lib64" >> ~/.bashrc
source ~/.bashrc

run following to make nvidia-smi start faster

sudo nvidia-persistenced --persistence-mode

set up xvfb

sudo apt-get install xvfb
xvfb-run -s "-screen 0 1400x900x24" jupyter notebook

ref githubGist

TMUX

install

sudo apt install tmux

creat config file: subl /.tmux.conf

config

1. install ‘TMUX plugin manager(TPM)’ see TPM github for detail
2. for copy to system clipboard—install ‘tmux-yank’ plugin
3. other configurations see my backup file

reference

tmux shortcuts & cheatsheet

a pretty tmux config